Matemática: 2010

Trinômio Quadrado Perfeito

Determinaremos o produto notável responsável pela formação do trinômio x² + 2xy + y² ou x² – 2xy + y². Observe:

x² + 18x + 81 → (x + 9)²
√x² = x
√81 = 9
(x + 9)² = (x + 9) * (x + 9) = x² + 9x + 9x + 81 = x² + 18x + 81

4x² – 48x + 144 → (2x – 12)² √4x² = 2x
√144 = 12
(2x + 12)² = (2x + 12) * (2x + 12) = 4x² + 24x + 24x + 144 = 4x² + 48x + 144

Fatoração por Agrupamento

Na fatoração por agrupamento, utilizamos inicialmente a fatoração por evidência e logo em seguida agrupamos os termos sob certas condições também de evidenciação. Observe:

2yx – x – 6y + 3, aplicar evidência entre 2yx e –x e entre –6y e 3.

2yx – x → x * (2y – 1)

–6y + 3 → –3 * (2y – 1)

2yx – x – 6y + 3 → x * (2y – 1) – 3 * (2y – 1) → (x – 3) * (2y – 1)

Observe mais exemplos:

bx – 2b + x – 2 → bx + x – 2b – 2 → x * (b + 1) – 2 * (b + 1) → (x – 2) * (b + 1)

10x² + 15xy + 4x + 6y → 10x² + 4x + 15xy + 6y → 2x * (5x + 2) + 3y * (5x + 2) → (2x + 3y) * ( 5x + 2)

Diferença entre dois quadrados
Nessa fatoração aplicaremos a raiz quadrada entre os elementos. O valor resultante das raízes formará uma multiplicação entre binômios no mesmo modelo do notável produto da soma pela diferença. Veja:

4x² – 16 → (2x + 4) * (2x – 4) √4x² = 2x
√16 = 4

25x² – 100 → (5x + 10) * (5x – 10) √25x² = 5x
√100 = 10

81x4 – 144 → (9x² + 12) * (9x² – 12) √81x4 = 9x²
√144 = 12

400x² – 49 → (20x + 7) * (20x – 7) √400x² = 20x
√49 = 7

Fatoração de Polinômios

Fatorar um número significa escrevê-lo na forma de produto de números primos. Por exemplo, a fatoração do número 36 consiste na multiplicação entre os números 2 * 2 * 3 * 3. Na fatoração de polinômios devemos escrever o mesmo através do produto entre outros polinômios.
As fatorações mais conhecidas são: fator comum em evidência, agrupamento, diferença entre dois quadrados, trinômio quadrado perfeito e trinômio soma eproduto.

Fator comum em evidência
Nesse modelo de fatoração temos que determinar o elemento comum aos termos que formam o polinômio. Observe:

No polinômio x² + 2x, temos que a variável x é comum aos dois termos. Ela será o termo em evidência, a qual dividirá todos os termos do polinômio original.

x² + 2x → x * (x + 2)
x² : x = x
2x : x = 2

Veja mais exemplos de fatoração por evidência:

4x³ – 2x² → 2x² * (2x – 1)
4x³ : 2x² = 2x
2x : 2x = 1

16x² + 8 → 8 * (2x² + 1)
16x² : 8 = 2x²
8 : 8 = 1

Produtos Notáveis

Quadrado da soma de dois termos

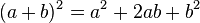$(a+b)^2= a^2+2ab+b^2 \,$ .

Regra básica: Quadrado do primeiro, mais duas vezes o primeiro vezes o segundo, mais o quadrado do segundo.

Exemplos:

$\left( \frac{4x}{5y}+z \right )^2=\frac{16x^2}{25y^2}+\frac{8xz}{5y}+z^2$
$(8x+a)^2=64x^2+16ax+a^2 \,$

Quadrado da diferença de dois termos

A expressão diferença do quadrado da soma apenas pelo sinal da segunda parcela:

Regra básica: Quadrado do primeiro termo, menos duas vezes o primeiro vezes o segundo , mais o quadrado do segundo

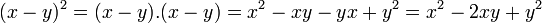
$(x - y)^2 = (x -y) . (x - y) = x^2 - xy - yx + y^2 = x^2 - 2xy + y^2 \,$

Exemplos:

$\left( \frac{3m}{4n}-p \right )^2=\frac{9m^2}{16n^2}-\frac{6mp}{4n}+p^2$
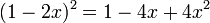
Produto da soma pela diferença de dois termos
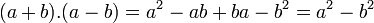$(a + b).(a - b) = a^2 - ab + ba - b^2=a^2-b^2 \,$
Regra básica: Quadrado do primeiro termo menos o quadrado do segundo termo
- Exemplos:
1. $(a^2+b^3).(a^2-b^3)=a^4-b^6 \,$
2. $\left( \frac{a}{x}-2 \right ).\left( \frac{a}{x}+2 \right )=\frac{a^2}{x^2}-4$

Polinômios

Polinômio é uma expressão algébrica composta por dois ou mais monômios
* Soma e Subtração

veja: (4x² - 5x + 6) + (7x² - 4) + (3x - 18)
   4x² - 5x + 6 + 7x² - 4 + 3x - 18
   11x² - 2x - 16

- Podemos eliminar os parênteses só se os termos forem semelhantes. Pois trata-se de soma e subtração de polinômios.

* Multiplicação

veja: (3x + 40) . (2x + 30)
   6x² + 90x + 80x + 1.200
   6x² + 170x + 1.200

* Divisão

Caso queira verificar se a divisão está correta, basta multiplicar o quociente pelo divisor, com vistas a obter o dividendo como resultado

Potênciação com monômios

São várias as propriedades que formam as regras de potenciação de números reais, duas delas irão ajudar na compreensão da resolução de potência que envolve monômio. Essas propriedades dizem o seguinte:

Potência de um produto (a . b)^m = a^m . b^m

Potência de potência (a^m)ⁿ = a^m ^{. n}

Iremos aplicar essas duas propriedades no cálculo de potência de monômios. Por exemplo:

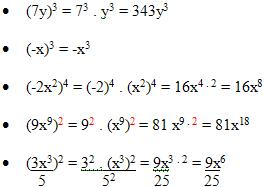Esses exemplos têm como resultado monômios, veja uma potenciação de monômio onde o resultado não será um monômio e sim, uma fração algébrica.

Dessa forma, podemos dizer que sempre que o expoente for negativo o resultado da potência será uma fração algébrica.

Monômios

Expressão algébrica definida apenas pela multiplicação entre o coeficiente e a parte literal. Exemplos:

2x, 4ab, 10x², 20xyz, 30abc, 2z, y, b³, 100ax³

Monômios semelhantes
Expressões algébricas que possuem a parte literal semelhante.
Exemplos:

2x e 4x
7x² e 8x²
10ab e 3ab
2ya e 6ya
7bc e 9cb
100z e 20z
Adição e subtração de monômio

A adição e a subtração de monômio devem ser efetuadas quando as partes literais são semelhantes. Exemplos:

2a + 7a = 9a
5x – 2x = 3x
10ab – 9ab = ab
6y – 9y = – 3y
7bc + 3cb = 10bc ou 10cb
– 12xy – 10xy = – 22xy

Multiplicação entre monômios
Ao multiplicar monômios em que as partes literais são semelhantes devemos seguir os seguintes passos:
1º passo: multiplicar os coeficientes
2º passo: conservar a parte literal e somar os expoentes.

Exemplos:

2x * 2x = 4x²
4xy * 6xy² = 24x²y³
10a²b * 9a²b³ = 90a⁴b⁴
5xyz * 6x²y³z = 30x³y⁴z²

Ao multiplicar monômios com parte literal diferente devemos:
1º passo: multiplicar os coeficientes
2º passo: se as letras são diferentes, agrupe-as
Exemplo:
2x * 3y = 6xy
4ab * 5z = 20abz
20c * 2ab = 40abc
x * 6a = 6xa

Divisão entre monômios

Parte literal semelhantes
1º passo: dividir os coeficientes.
2º passo: conservar a parte literal e subtrair os expoentes.

Exemplo:
5x³ : 5x² = x
10x²y² : 2x = 5xy²
30z : 5z = 6
20b³ : 10b = 2b²

Expressões algébricas

No cotidiano, muitas vezes usamos expressões sem perceber que as mesmas representam expressões algébricas ou numéricas.

Numa papelaria, quando calculamos o preço de um caderno somado ao preço de duas canetas, usamos expressões como 1x+2y, onde x representa o preço do caderno e y o preço de cada caneta.

Num colégio, ao comprar um lanche, somamos o preço de um refrigerante com o preço de um salgado, usando expressoes do tipo 1x+1y onde x representa o preço do salgado e y o preço do refrigerante.

Usamos a subtração para saber o valor do troco. Por exemplo, se V é o valor total de dinheiro disponível e T é o valor do troco, então temos uma expresão algébrica do tipo V-(1x+1y)=T.

As expressões algébricas são encontradas muitas vezes em fórmulas matemáticas. Por exemplo, no cálculo de áreas de retângulos, triângulos e outras figuras planas.

Expressão algébrica	Objeto matemático	Figura
A = b x h	Área do retângulo
A = b x h / 2	Área do triângulo
P = 4 a	Perímetro do quadrado

Exemplos:

Consideremos P=2A+10 e tomemos A=5. Assim
```
P = 2.5+10 = 10+10 = 20
```
Aqui A é a variável da expressão, 5 é o valor numérico da variável e 20 é o valor numérico da expressão indicada por P. Observe que ao mudar o valor de A para 9, teremos:
```
A = 2.9 + 10 = 18 + 10 = 28
```
Se A=9, o valor numérico de P=2A+10 é igual a 28.
Conclusão: O valor numérico de uma expressão algébrica é o valor obtido na expressão quando substituímos a variável por um valor numérico.

Matemática

quarta-feira, 14 de julho de 2010